문제

Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.

이진 검색 트리가 주어지면 kthSmallest 함수를 작성하여 k 번째 가장 작은 요소를 찾으십시오.

Note :

You may assume k is always valid, 1 ≤ k ≤ BST’s total elements.

Example 1 :

Input : root = [3,1,4,null,2], k = 1

   3
  / \
 1   4
  \
    2

Output : 1

Example 2 :

Input : root = [5,3,6,2,4,null,null,1], k = 3

       5
      / \
     3   6
    / \
   2   4
  /
 1

Output : 3

기본 지식

binary search tree 특징 :

이진 트리이기 때문에, 최대 두 개의 자식 노드를 가진다.
각 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
각 노드의 오른쪽 서브트리에는 그 노드의 값과 같거나 큰 값들을 지닌 노드들로 이루어져 있다.

트리 순회(tree traversal) :

트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말하는 데, 대표적으로 세가지 방법이 있습니다.

pre-order : 기준을 루트 노드로 했을 때, 먼저(pre)들린다 해서 pre-order방식이고, 방문 순서는 Root - Left - Right 입니다.

Root 를 방문한다
왼쪽 subtree를 방문한다
오른쪽 subtree 를 방문한다

PreOrderTraversal( Node* pNode ){

if( pNode != m_pNodeTail )

	{

	visit(pNode); // 1. Root 를 방문한다

	PreOrderTraversal(pNode->pLeft ); // 2. 왼쪽 subtree를 방문한다

	PreOrderTraversal(pNode->pRight ); // 3. 오른쪽 subtree 를 방문한다

	}
	
}

in-order : 루트노드가 안(in)에 있다고 해서 in-order방식이고, 방문 순서는 Left - Root - Right 입니다.

post-order : 루트노드가 마지막(post)에 있다고 해서 post-order방식이고, 방문순서는 Left - Right - Root 입니다.

풀이

위의 문제를 해결하기 위해서 가장 중요한 것은 배열에 숫자 크기대로 “정렬” 해야합니다. 하지만, 이진 검색 트리 특징을 이용하여 in-order 방식으로 순회하게 되면 저절로 오름차순으로 수를 리턴하게 됩니다. 왜냐하면 in-order방식의 방문순서는 Left - Root - Right 인데, 이진 검색 트리는 왼쪽 서브 트리에 작은 수가 있기 때문입니다.

Answer :

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int i = 0;
    int result;
    
    public int kthSmallest(TreeNode root, int k) {
    
        inorder(root,k);
        
        return result;
    }
    
    public void inorder(TreeNode root, int k){
        if( root==null ) return;	// 재귀호출의 종결 조건
        
        inorder(root.left,k);		// Left
        
        i++;				// 
                                        // Root
        if(i == k){			//
            result = root.val;		// 
        }				            
        
        inorder(root.right,k);		// Right
    }
}

위의 코드에서 해당 노드(Root)를 방문할 때 i가 증가하므로 i가 즉, 문제의 k와 같습니다. 따라서 i와 k가 일치할 때 result값이 k번째로 작은수가 됩니다.

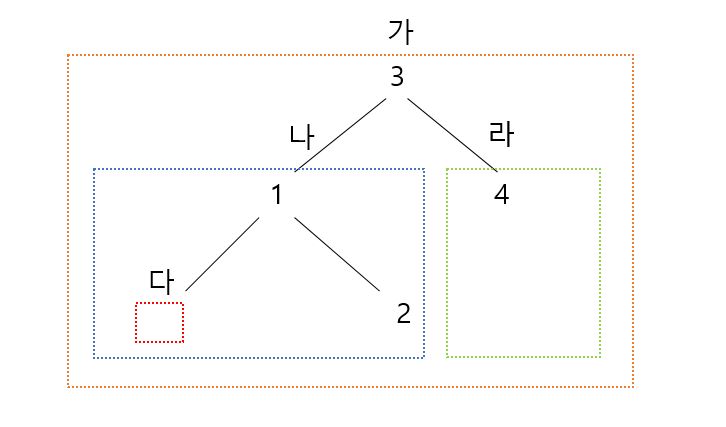예제 노드

노드 방문순서 :

(가)노드의 Left서브트리(나)를 찾아간다
(나)노드의 Left서브트리(다)를 찾아간다
(다)노드는 null 이기 때문에 재귀호출의 종결조건으로 return하고 끝난다
(나)노드의 Root 차례로 i가 증가한다
(나)노드의 Right서브트리(2)를 찾아간다
2의 Left서브트리를 찾아가고 null이므로 return, Root차례에서 i가 증가, Right서브트리를 찾아가고 null 이므로 return
(가)의 Left서브트리인 (나)의 Left,Root,Right 순서가 끝났으므로 (가)의 Root(3)을 방문하고 i가 증가한다
(가)의 Right서브트리(라)를 찾아간다
(라)의 Left서브트리를 찾아가고 null이므로 return, Root(4)를 방문하고 i가 증가, Right서브트리를 찾아가고 null이므로 return

이진 검색 트리 특징상 in-order순회로 방문할 때 저절로 오름차순으로 방문(Root)합니다. 따라서 각각 i가 증가할 때, i가 증가하고 난 후 k와 비교해서 같으면 방문한 노드(Root)의 값(root.val)을 반환하기 때문에, k번째 작은수가 됩니다.

출처 : 제가 알고리즘 문제에 막 감을 익히고 있는 단계여서 유튜버 승지니어님의 코드를 많이 인용하였습니다. 도움되는 영상이 많이 있으므로 많은 방문 부탁드리겠습니다.

유튜브 승지니어 해당영상

← Previous Post Next Post →

LeetCode#230

Kth Smallest Element in a BST

문제

기본 지식

풀이