문제

Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.

Calling next() will return the next smallest number in the BST.

이진 검색 트리 (BST)를 통해 iterator를 구현하십시오. iterator는 BST의 루트 노드로 초기화됩니다.

next()를 호출하면 BST에서 가장 작은 다음 번호가 반환됩니다.

Example :

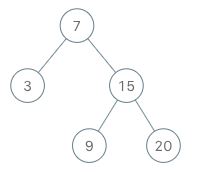
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // return 3
iterator.next();    // return 7
iterator.hasNext(); // return true
iterator.next();    // return 9
iterator.hasNext(); // return true
iterator.next();    // return 15
iterator.hasNext(); // return true
iterator.next();    // return 20
iterator.hasNext(); // return false

Note :

next() and hasNext() should run in average O(1) time and uses O(h) memory, where h is the height of the tree.
You may assume that next() call will always be valid, that is, there will be at least a next smallest number in the BST when next() is called.
next() 및 hasNext()는 평균 O(1) 시간으로 실행되어야하며 O(h) 메모리를 사용합니다. 여기서 h는 트리의 높이입니다.
next() 호출이 항상 유효하다고 가정 할 수 있습니다. 즉 next()가 호출 될 때 BST에 최소한 다음으로 작은 숫자가있을 것입니다.

기본 지식

binary search tree 특징 :

이진 트리이기 때문에, 최대 두 개의 자식 노드를 가진다.
각 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
각 노드의 오른쪽 서브트리에는 그 노드의 값과 같거나 큰 값들을 지닌 노드들로 이루어져 있다.

트리 순회(tree traversal) :

트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말하는 데, 대표적으로 세가지 방법이 있습니다.

pre-order : 기준을 루트 노드로 했을 때, 먼저(pre)들린다 해서 pre-order방식이고, 방문 순서는 Root - Left - Right 입니다.

Root 를 방문한다
왼쪽 subtree를 방문한다
오른쪽 subtree 를 방문한다

PreOrderTraversal( Node* pNode ){

if( pNode != m_pNodeTail )

	{

	visit(pNode); // 1. Root 를 방문한다

	PreOrderTraversal(pNode->pLeft ); // 2. 왼쪽 subtree를 방문한다

	PreOrderTraversal(pNode->pRight ); // 3. 오른쪽 subtree 를 방문한다

	}
	
}

in-order : 루트노드가 안(in)에 있다고 해서 in-order방식이고, 방문 순서는 Left - Root - Right 입니다.

post-order : 루트노드가 마지막(post)에 있다고 해서 post-order방식이고, 방문순서는 Left - Right - Root 입니다.

콜스택(call stack) :

컴퓨터 프로그램에서 현재 실행 중인 서브루틴에 관한 정보를 저장하는 스택 자료구조이다.

풀이

binary search tree를 in-order 순회하면 오름차순으로 작은 수부터 차례대로 방문을 하게 됩니다. binary search tree 특징상 작은 수는 left 큰 수는 right sub tree에 배치되어 있는데, in-order 순회 방식은 left - root - right 순서로 방문하기 때문입니다. 이와 연관된 문제 leetcode230를 보시면 이해가 더 쉽게 될 것입니다.

위의 문제는 순회로 재귀 호출을 구현하기보다는 call stack 방식으로 작업 내용을 스택에 저장하여 해결하는 방법으로 설명해 드리겠습니다. (note: O(h) 공간을 사용, 최대 스택의 크기는 h:높이)

Answer :

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class BSTIterator {
    Stack<TreeNode> stack = new Stack<>();
    public BSTIterator(TreeNode root) {
        while(root!=null){
            stack.push(root);
            root = root.left;
        }
    }
    
    /** @return the next smallest number */
    public int next() {
        TreeNode node = stack.pop();
        if(node.right != null){
            TreeNode cur = node.right;
            while(cur!=null){
                stack.push(cur);
                cur = cur.left;
            }
        }
        return node.val;
    }
    
    /** @return whether we have a next smallest number */
    public boolean hasNext() {
        return !stack.isEmpty();
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * int param_1 = obj.next();
 * boolean param_2 = obj.hasNext();
 */

BSTIterator iterator = new BSTIterator(root);

root(7)을 스택에 push( )후, 왼쪽서브트리(3)로 이동
```
 stack : 7
```
root(3)을 스택에 push( )후, 왼쪽서브트리로 이동(null종료)
```
 stack : 7 3
```
in-order (Left - Root - Right)의 Left작업을 모두 스택에 저장
TreeNode node = stack.pop();

return node.val;

스택에 저장된 작업내용을 바탕으로 in-order (Left - Root - Right)의 Root작업을 실행, 3을 pop( ) return 3
```
stack : 7
```
3은 오른쪽 서브트리가 없기 때문에 if문을 그냥 통과
다음 작업내용(7)을 pop( ) return 7
```
 stack :
```
7의 오른쪽 서브트리(15) push( )후 왼쪽 서브트리로 이동(똑같이 in-order순회 적용)
```
 stack : 15
```
왼쪽 서브트리가 null이 아니기 때문에 while문 한번 더 호출

9 push( )
```
 stack : 15 9
```
다음 작업내용(9)을 pop( ) return 9

오른쪽 서브트리가 없기 때문에 if문 통과
```
 stack : 15
```
다음 작업내용(15)을 pop( ) return 15

오른쪽 서브트리(20) push( )후 왼쪽 서브트리로 이동(똑같이 in-order순회 적용)

왼쪽 서브트리는 null로 while문 통과
```
 stack : 20
```
다음 작업내용(20)을 pop( ) return 20

오른쪽 서브트리가 null이므로 모든 작업 종료

출처 : 제가 알고리즘 문제에 막 감을 익히고 있는 단계여서 유튜버 승지니어님의 코드를 많이 인용하였습니다. 도움되는 영상이 많이 있으므로 많은 방문 부탁드리겠습니다.

유튜브 승지니어 해당영상

← Previous Post Next Post →

LeetCode#173

Binary Search Tree Iterator

문제

기본 지식

풀이